Michelis-Menten Equation Calculator
Discover the kinetics of a one-substrate reaction catalysed by an enzyme using the Michaelis-Menten Equation Calculator. Calculating the Michaelis-Menten constant, reaction rate, substrate concentration, and maximal rate of reaction is beneficial. Simply enter the Michaelis constant, maximal reaction speed, and substrate concentration information, then click the calculate button to see the reaction rate.
Michelis-Menten Equation Calculator: This calculator calculates the rate of an enzyme's response in a short period of time. In this article, you'll learn everything you need to know about Michaelis-Menten enzyme kinetics, the Michelis Menten equation, how to utilise it, and how to get the Michaelis constant. Continue reading to receive the sample questions and answers.
Michaelis-Menten Equation
Here is the Michaelis-Menten Equation for determining an enzyme's reaction rate V= VmaxS/(Km +S)
- Where, V = rate of reaction
- Vmax = maximum reaction speed
- [S] = substrate concentration
- Km = Michaelis constant
Michaelis Menten Equation Derivation and Applications
The Michaelis-Menten model is based on a kinetic idea that can be stated in the enzyme equation below: E + S ⇄ ES → E + P
- Where,
- E = Enzyme;
- S = Substrate; and
- P = Product.
The enzyme binds to the substrate, resulting in the formation of a product. Because the enzyme can bind and unbind with a variety of substrates several times, this reaction occurs in both directions. This notation combines three enzyme kinetics equations into a single symbol.
- E + S → ES, speed of the reaction: k₁;
- ES → E + S, speed of the reaction: k₂; and
- ES → E + P, speed of the reaction: k₃.
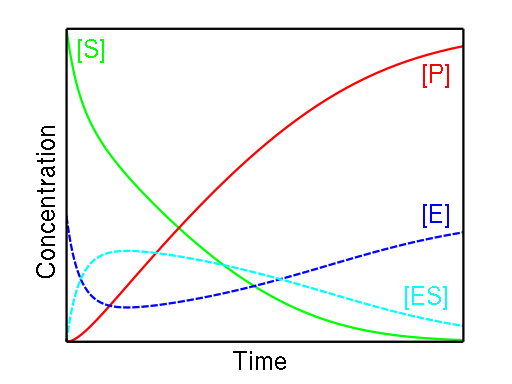
During the duration of a reaction, the amount of ES remains generally constant until the amount of substrate is near zero. The formula utilised in our Michaelis-Menten equation calculator was developed based on two key observations:
- When the substrate concentration is low, the equation's speed is proportional to the substrate; and when the substrate concentration is high, the equation's speed is proportional to the substrate.
- The speed becomes independent and does not exceed the maximum rate when the substrate level is high.
Michaelis and Menten had to come up with a new constant to explain the ES complex's stability, and it had to be in the same unit as the substrate.
How to Find Michaelis Constant Km?
Look at how to use the Menten equation Michaelis to determine the Michaelis Menten constant.
- Step 1: Get the highest response rate, the highest substrate concentration, and the fastest reaction rate.
- Step 2: Multiply the substrate concentration by the maximum reaction speed.
- Step 3: The reaction rate is multiplied by the substrate concentration once again.
- Step 4: Take the second product and subtract it from the first.
- Step 5: The Michaelis Constant is found by dividing the result by the reaction rate.
Michelis-Menten Equation Examples
Question 1: The Michaelis constant for an enzyme-catalyzed reaction is 0.5 M, the substrate concentration is 2.0 M, and the maximal reaction speed is 2.1 1/s. Determine the enzyme's reaction rate under these conditions.
Solution:
Given
Michaelis constant = 0.5 M
Substrate concentration = 2.0 M
Maximum reaction speed = 2.1 1/s
Michaelis-Menten Equation is V = (Vmax * [S]) / ([S] + Km)
V = (2.1 x 2.0)/(2.0 + 0.5)
= 4.2/2.5
= 1.68 1/s
Hence, the reaction rate is 1.68 1/s.
FAQs on Michelis-Menten Equation
1. What are the Michaelis Menten equation's limitations?
The Michaelis–Menten equation does not hold when there is a substrate inhibition or activation due to the binding of a second substrate molecule. The existence of many intermediates and their durations are not described in the steady-state and rapid equilibrium kinetics.
2. What can be learned from the Michaelis Menten equation?
A set of first-order differential equations can be used to illustrate the process described by the Michaelis–Menten equation. The rate of change of each substance in these differential equations is defined as the rate constant multiplied by the concentration of each molecule in the chemical equation.
3. What does Michaelis constant tell us?
The Michaelis-Menten constant, Km, indicates the concentration of the substrate when the reaction velocity is half that of the reaction's maximum velocity. It's also known as binding affinity, and it's a measurement of how effectively a substrate binds with a certain enzyme.
4. What impact do inhibitors have on the Michaelis-Menten equation?
So, as you can see from the final rate expression, a competitive inhibitor changes the Michaelis constant KM, making the enzyme appear to have a lower affinity for the substrate (higher KM = lower affinity). This makes sense because the inhibitor binds to the same location as the substrate.